【導讀】我們將研究CCM反激式轉(zhuǎn)換器于電壓模式下被漏電感影響的小信號響應。我們將從大信號模型逐步邁向逐漸簡化的小信號電路原理圖,以建立最簡單的線性版本。從這最終的電路,我們將提取控制-輸出傳遞函數(shù),并顯示漏電感如何影響傳遞函數(shù)分母的品質(zhì)因數(shù)。
從大信號到小信號
當您想獲得一個復雜電路的傳遞函數(shù)時,您的目標是減少復雜度,以便通過最簡單的電路原理圖進行分析。但是,當您在減少電路的過程中–通過因式分解、簡化表達式、忽略變量等–您必須測試您的新電路,并與最初的電路響應進行比較。在最初的響應和您隨后的簡化版本的響應之間的任何偏差都表明您弄錯了,或者您作的假設過于簡單化 :丟棄這電路并回到前一步重做。遵照這步驟,您肯定進展很慢,但卻很仔細,您可立即發(fā)現(xiàn)和改正錯誤。沒有什么比在結(jié)束時發(fā)現(xiàn)錯誤而同時您意識到在一個中間步驟就出了問題更令人沮喪的了!

圖1:這開環(huán)大信號電路原理圖是我們的起始電路,其動態(tài)響應將用作后面步驟的參考
首先我們用第二部分介紹的小信號版本代替大信號PWM開關(guān)模型。然后,我們可運行一個交流仿真,并驗證操作點和響應是相同的。非線性模型在圖1中,而小信號版本出現(xiàn)在圖2中。占空比已分為兩個源,一個用于靜態(tài)占空比,一個用于交流調(diào)制。
偏置點與圖1中的相同說明第一步是正確的。我們來看看這兩個比較電路的頻率響應如何。我們已采集了如圖3 的波特圖:幅值和相位曲線重疊,驗證了我們的第一步。
圖2中的電路圖是正確的但相當復雜。如上所述,小信號分析意味著盡可能簡化電路,并將各種不同元件重新整理成一個更有意義的架構(gòu)。

圖2:PWM開關(guān)由小信號版本替代,并對參考頻率響應進行了電路動態(tài)響應檢查

圖3:兩個電路的波特圖完全重疊,驗證了第一步。
我們插入的PWM開關(guān)模型確實是線性版本,我們無需研究它。然而,計算峰谷電流、鉗位電壓等的所有源仍然是大信號運算,我們需要將其線性化。幸運的是,這有些源在我們的交流分析中是不需要的的如Ip和d2。
源線性化
您有兩個選擇,如果您想線性化這些源。您可通過小的勵磁改變每一變量–您看到的某些變量中的小帽子^ - 并整理交流和直流項以形成兩個獨立的等式:一個靜態(tài)和一個動態(tài)的表達式。靜態(tài)的表達式描述了操作點–此處我們并不需要它–而動態(tài)的表達式是我們想要的。采用這技術(shù)的問題是您獲得的項和交叉產(chǎn)品的數(shù)量,特別是變量超過兩個。整理這些項以形成交流和直流等式,有時可能是繁瑣的和錯誤的源。我們試著采用谷底電流的定義:
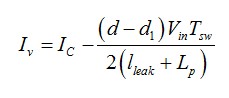 (1)
(1)這里有3個變量,Ic, d 和d1。如果我們少量改變每一變量,得出
 (2)
(2)展開為
 (3)
(3)現(xiàn)在合并交流和直流項,我們有兩個定義:
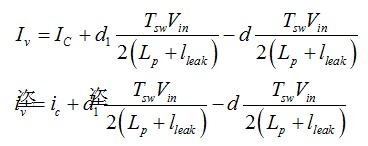 (4)
(4)如果我們定義兩個系數(shù)kivd 和kivd1為
 (5)
(5) (6)
(6)(4)中的動態(tài)等式可重新整理為
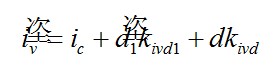 (7)
(7)靜態(tài)系數(shù)kivd 和kivd1將被作為參數(shù)在捕獲的電路圖中傳遞,并在仿真開始前預估。
另一現(xiàn)有的選擇是不用整理而以更快的方式獲得小信號系數(shù)如kivd 和kivd1。分步操作是簡單的,但表達式很復雜,并有多個變量,它很快成為困難的工作,您無法通過解算器如Mathcad?自動求解。一組不相關(guān)(獨立) 的變量給出更快的方法,包括使用偏微分法,如下所示:
 (8)
(8)或使用小信號記法
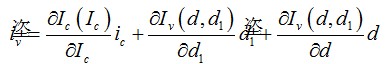 (9)
(9)在這里,交流項系數(shù)只有從這偏微分法獲得。將該方法應用到圖2中的d1發(fā)生器得出
 (10)
(10)從中導出
 (11)
(11)考慮kd1vo 和kd1iv系數(shù),我們可將(11)改寫為
 (12)
(12)其中
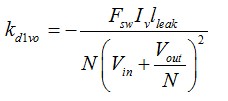 (13)
(13) (14)
(14)現(xiàn)在我們有線性的d1 和Iv源,我們可更新和簡化電路圖圖2。結(jié)果如圖4:在參數(shù)文本窗口中計算表達式(5)、(6)和(13)、(14)?,F(xiàn)在這圖中的所有源都是小信號類型。快速的交流分析顯示,頻率響應的幅值和相位完全與圖3匹配。
簡化電路原理圖
我們可從這電路原理圖開始分析線性轉(zhuǎn)換器。不過可能需要進一步的簡化和整理。例如,在控制-輸出傳遞函數(shù)中,輸入電壓是Vin恒定的,
因此,連接到輸入電壓的節(jié)點“a”正好接地。通過接地節(jié)點“a”,您可重畫電路并顯示為如圖5所示的更簡單的版本。測試這電路的頻率響應并與圖3比較,以檢測在新整理出的模型中的任何錯誤。
電流源B7與電壓源B1串聯(lián)。為進一步簡化,B7負端可參考接地,而B1的輸出連接到節(jié)點20以獨立的源轉(zhuǎn)換。圖6給出了新的電路圖。節(jié)點20用于源B10(通過定義更新),兩個電流源B7/B2可并聯(lián)以形成單個源。這是如圖7所示的用于分析的最終電路。請注意源Iv表達式已包含在d1源中?;趫D8中的大信號參考模型繪制此電路的頻率響應。因為相位和幅值相同,我們現(xiàn)在可著手這最終的表達式。

圖4:更新的電路現(xiàn)在只包括線性源。
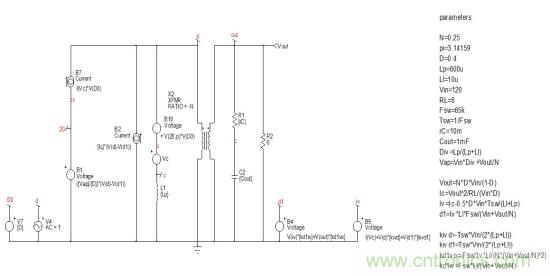
圖5:考慮恒定的輸入電壓,節(jié)電“a”可接地并進一步簡化,得出小信號電路。

圖6:電流源B7現(xiàn)在接地,而B1在節(jié)點20提供電壓。
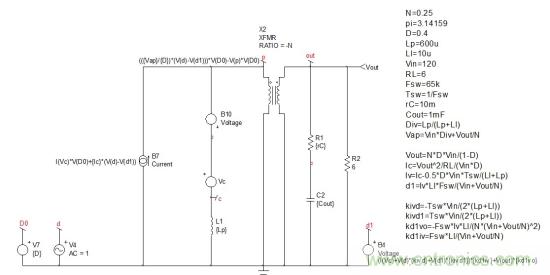
圖7:只要電流源并聯(lián)到B7和節(jié)點20整合到B10,我們可得出最終的小信號電路原理圖。Iv已整合到d1。

圖8:大信號模型的頻率響應和我們簡化電路圖7的頻率響應相同
生成等式
我們從電感電流等于節(jié)點“c”的電壓除以電感阻抗開始。節(jié)點“c”的電壓由節(jié)點“p”的電壓與電壓源B10串聯(lián)定義。節(jié)點“p”的電壓只是減去通過變壓器匝數(shù)比N(忽略二極管正向壓降)反射到初級端的輸出電壓。我們有
 (15)
(15)源d1可改寫,因為Lp的電流現(xiàn)已被定義(它是圖7 d1源的I(Vc))
 (16)
(16)解得d1(s)為
 (17)
(17)輸出電流是以變壓器匝數(shù)比N縮放的初級電流。它是由源B7減去流經(jīng)電感的電流及由(15)定義的電流:
 (18)
(18)在此表達式中,Ic是在本系列文章第二部分已確定的直流值
 (19)
(19)這電流以由如圖9所示的rC,Cout和負載電阻RL形成的阻抗循環(huán)。
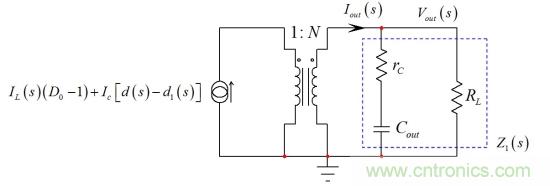
圖9:最終描述包括變壓器驅(qū)動由輸出電容、ESR和負載電阻形成的復雜的阻抗RL。
這輸出電流也可定義為
 (20)
(20)阻抗可通過將rC + Cout和RL并聯(lián)或應用快速分析電路技術(shù)(FACTS)迅速得出。重新整理結(jié)果,您應發(fā)現(xiàn)
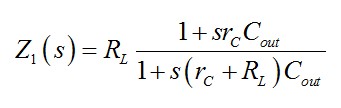 (21)
(21)現(xiàn)在結(jié)合(18)、 (20) 和(21),我們可寫
 (22)
(22)現(xiàn)在的樂趣在于求解Vout,并以二階多項式的形式重新整理傳遞函數(shù)。通過Mathcad的幫助,我們得出:
 (23)
(23)其中我們已確定以下原系數(shù)

文獻中給出的典型的反激式轉(zhuǎn)換器的傳遞函數(shù)按照(23)的形式并采用下面的定義:

測試解析表達式
如果我們假設圖1的運行值,并繪制由(23)給出的響應,無論是lleak為0 (rC= 0歐)的復雜系數(shù)還是簡化的反激式表達式,幅值和相位曲線如圖10所示都完全重疊。

圖10:當漏電感設為0,采用復雜系數(shù)的等式和傳統(tǒng)的反激式表達式返回相同的頻率響應曲線。
接下來的測試包括設置lleak為10 μH、疊合由Mathcad和小信號SPICE仿真得出的曲線。如圖11所示,曲線的完美重疊證實了我們對傳遞函數(shù)考慮漏電感的數(shù)學推導。

圖11:SPICE和Mathcad繪制出完全重疊的曲線,證實了我們圖4的關(guān)于傳遞函數(shù)中Vout結(jié)合d的分析推導。
最后,為將我們的建模方案與另一個仿真平臺比較,我的同事Dr. Capilla采集了在第一部分介紹的以Simplis模板簡化的逐周期模型,并運行幾個配置以提取小信號響應。結(jié)果如圖13所示,其中我們已粘貼了采用小信號模型得到的SPICE仿真結(jié)果。
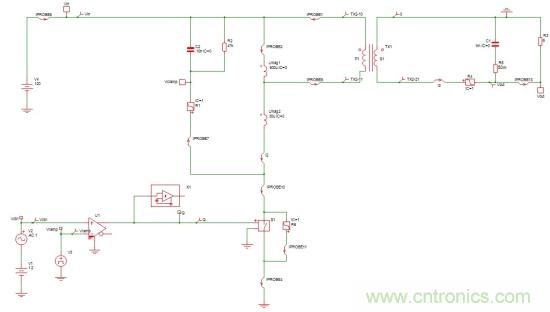
圖12:Simplis可提取開關(guān)電路的小信號響應

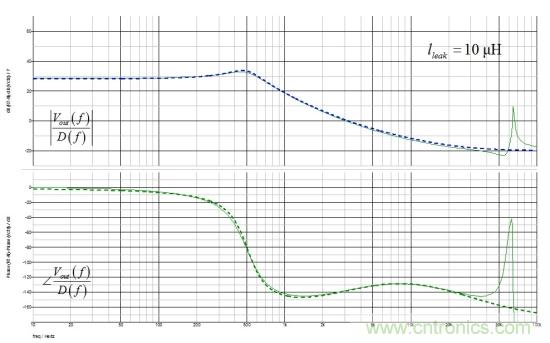

圖13:Simplis的交流響應顯示相較SPICE平均模型略有阻尼的電路
對于1-μH漏電感值,Simplis顯示出稍低的Q,可能是由于仿真電路中一些選定的開關(guān)元件固有的損耗。對于較高的漏電感值(10和30 μH),符合得非常好,曲線幾乎重疊。
漏電感和品質(zhì)因數(shù)
現(xiàn)在我們的模型是正確的,我們可交流掃描圖1電路,并看漏電感如何影響幅值和相位曲線。在具低漏電感時,Q很明顯,超過10 dB。當漏電感增加,每切換周期損耗更多能量,品質(zhì)因數(shù)減弱。對于大電感值30 μH,系統(tǒng)變得過阻尼。
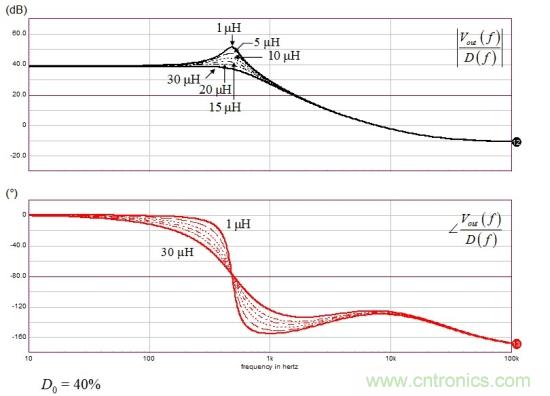
圖14:增加漏電感明顯阻尼工作于電壓模式的CCM反激式轉(zhuǎn)換器的響應。
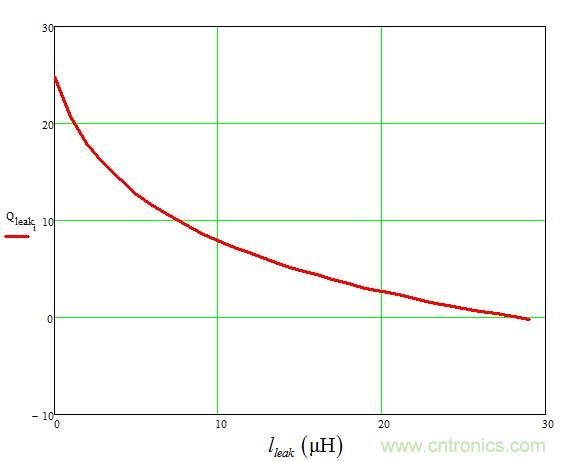
在圖15中,我們已繪制出Q相對漏電感的值,證實了它對反激式轉(zhuǎn)換器的阻尼效應。
在電流模式中,占空比截斷消失,因為盡管存在漏電感,但峰值電流不受影響,因為ton自然延長至符合峰值設定點。如[1]所寫,它可標明電流模式控制(CCM)中的開關(guān)占空比定義為
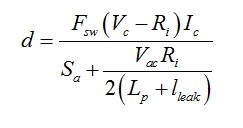 (24)
(24)其中Fsw是開關(guān)頻率,Vc是控制電壓,Ri是檢測電阻,Ic是如(19)定義的端點“c”的電流,Sa是外部補償斜率,Vac是端點“a”和“c”之間的電壓。雖然漏電感增加,但有效的占空比(開關(guān)占空比由漏電感磁化時間減少)保持相對穩(wěn)定。因此,主要是次級電流的延遲影響了輸出電壓。但輸出電壓的降低在電流模式控制中低于電壓模式轉(zhuǎn)換器(圖16)。

圖16:在電流模式中,峰值電流保持穩(wěn)定,導通時間自然延長以補償漏電感的存在。因此,不像電壓模式控制,輸出電壓幾乎不受影響。
結(jié)論
在這最后一部分,我們已描述了CCM反激式轉(zhuǎn)換器在電壓模式控制下的控制-輸出的傳遞函數(shù)。漏電感增加了鉗位源損耗并提供阻尼:傳統(tǒng)的等式?jīng)]有預測這一行為,必須推導新模型。進一步的線性化過程中,必須確定性的小信號傳遞函數(shù),表示漏電感對品質(zhì)因數(shù)的影響。但電流模式控制受漏電感的影響較小。參考[2]和[3]指出文獻意識到漏電感的影響,但在更新的傳遞函數(shù)表達式中沒有規(guī)范地定義這影響。本文完成了這一工作。
免責聲明:本文為轉(zhuǎn)載文章,轉(zhuǎn)載此文目的在于傳遞更多信息,版權(quán)歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權(quán)問題,請聯(lián)系小編進行處理。
推薦閱讀:







